前回はエクイティと期待値(EV)の定義とその違いについて説明しました。
今回はこれらのコンセプトについて、より実践的な観点から解説していきます。
フォールドエクイティの定義・計算方法
アグレッシブにベットやレイズをすることで相手プレイヤーをフォールドさせる見込みがあるとき、しばしば「フォールドエクイティがある」という言い方をします。
また、相手プレイヤーがショートスタックであったりコーリングステーションであったりする場合は、逆に「フォールドエクイティがない」という言うこともあるでしょう。
このようにフォールドエクイティは「相手をフォールドさせる見込み」といった意味で使われることがしばしばありますが、それは正確な定義ではありません。
フォールドエクイティ(FE)の定義は以下の式で表されます。
- FE=(相手プレイヤーがフォールドする確率)*(相手プレイヤーのエクイティ)
一つ具体的な状況を考えてみましょう。
BU(ボタン)はQTで3.5bbにオープン、SBはフォールドし、BBは55でコールしました。ヘッズアップです。
フロップはAK6です。BBはチェックし、BUはポットの半分のサイズのベットをしました。
この場合のBUのフォールドエクイティを考えてみます。
さて、まずはBUとBBのエクイティを見てみましょう。
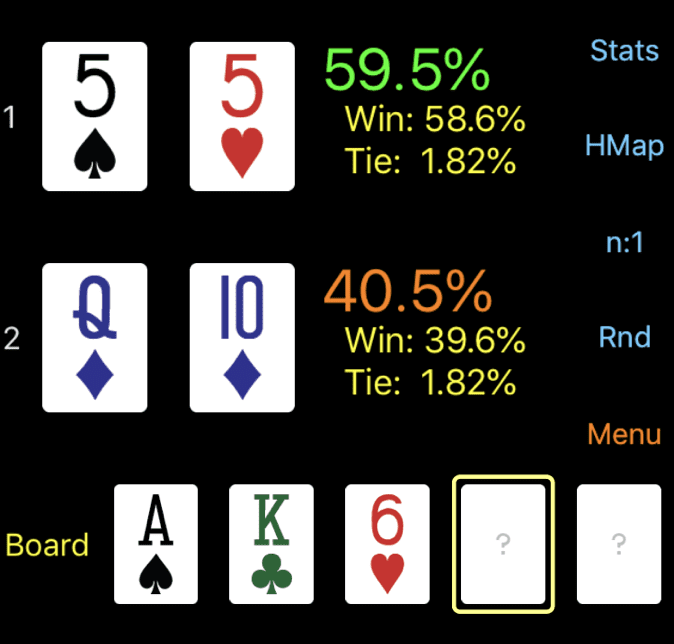
フロップではワンペアの55のほうが有利ですが、QTsはガットショット・ストレートドローがあり、さらにQやTもアウツになっているため、40.5%のエクイティがあります。
次に、BBがフォールドする確率を知る必要がありますが、これはBBのプレイやスタックサイズから予想するしかありません。
とはいえ全くの勘で予想するわけではなく、いくつかの考慮すべきポイントがあります。
- SPR(Stack To Pot Ratio:スタックとポットの比)
=SPRが1に近いほど(スタックサイズがポットに比べて小さいほど)、相手がフォールドする確率は低い。 - プレイスタイル
=コーリングステーションやアグレッシブなプレイヤーほど、フォールドする確率が低い。 - レンジとボードの噛み合い
=ボードに落ちているカードと相手のレンジにあるハンドが噛み合っている(ペアやドローができやすい)ほど、相手がフォールドする確率は低い。 - 自分のプレイスタイルのイメージ
=自分がブラフベットが多いプレイスタイルだと考えられているほど、相手がフォールドする確率は低い。
これらのポイントを考慮した上で、今回はBBのフォールド確率を次のように予想しました。
BBのスタックサイズは100bbで SPRは10以上だ。
BBのプレイスタイルはタイトアグレッシブで、OOPからのフロートはまだ一度も見せていない。OOPで勝つ見込みの薄いハンドを持っているときは素直にフォールドするタイプだ。
AK6rのフロップはオープンレンジに有利なボードだ。なぜなら、BBのプレイスタイルからして、彼が AA、KK、AJo+、A5s、A4s、KQsを持っているなら、プリフロップで3ベットを打つはずだからだ。ということは、Aや Kは彼のコールレンジよりも私のオープンレンジに多く入っていることになるだろう。
私はこのセッションでまだビッグブラフを見せていないから、ブラフが少ないと思われているかもしれない。
このように考え、今回はBBのフォールド確率を70%と予想しました。
これでフォールドエクイティを計算するための材料はすべてそろいました。定義の式に必要な数字を入れると、フォールドエクイティは次のようになります。
FE=(70%)*(59.5%)=41.65%
この41.65%というフォールドエクイティは、結局何を意味しているのでしょうか。
BBはフォールドすると、彼は本来持っていた60%のエクイティをすべて失い、代わりにBUがそのエクイティを得ることになります。
ただし、BUは60%のエクイティを常に得るわけではなく、あくまでもBBがフォールドした場合にのみ得ます。
ということは、BUがベットした瞬間のエクイティは、BUが本来持っているエクイティ(40.5%)にフォールドエクイティ(41.65%)が加算され、82.15%という非常に大きな数字になるのです。
つまり、フォールドエクイティとは、「相手プレイヤーがフォールドすることによる自分のエクイティの上昇分」と言い換えることもできます。
フォールドエクイティと本来のエクイティ(ポットエクイティとも言います)を合計して考えることで、ベットした時点でのエクイティを計算することができます。
ただし、前回で説明したとおり、エクイティと期待値(EV)は別物です。
ベットした時点でのエクイティはその瞬間の勝率であって、得られる見込みのあるチップや金額を表すEVではありません。
ベットに対して相手がコールまたはレイズをした場合は、フォールドエクイティはゼロになり、さらに相手のレンジから弱いハンドがある程度消えるので、自分の本来のエクイティ(ポットエクイティ)が減少します。
そのため、ベットした時点でのエクイティが十分高い場合、ベットのEVは少なくともプラスにはなりますが、ベットにコールやレイズをされたときにエクイティが大幅に下がる場合、ベットよりもチェックのほうがEVが高くなります。
ベット周りのエクイティとEVを考える際、この点には注意が必要です。
オールインブラフのEV計算
EVを計算するためには、勝率に基づいたポットの分け前に加えて、以後のアクションがどのように利益・損失に影響を与えるかを考慮する必要があります。
しかし、オールインの場合は以後のストリートにアクションの余地が残されておらず、あくまでもオールインに対してコールするかフォールドするかだけを考えれば済むため、計算が簡単になります。
例えば、プリフロップでのブラフオールインのEVはどのように計算すればよいでしょうか。
※クリックでgifが再生・停止します
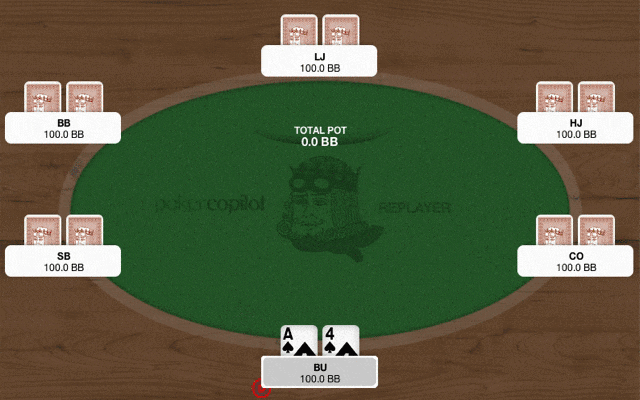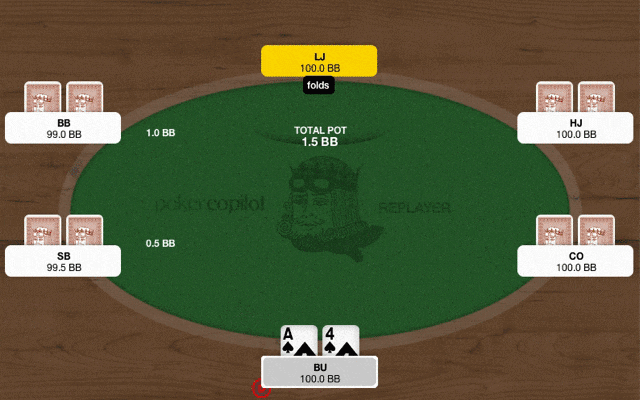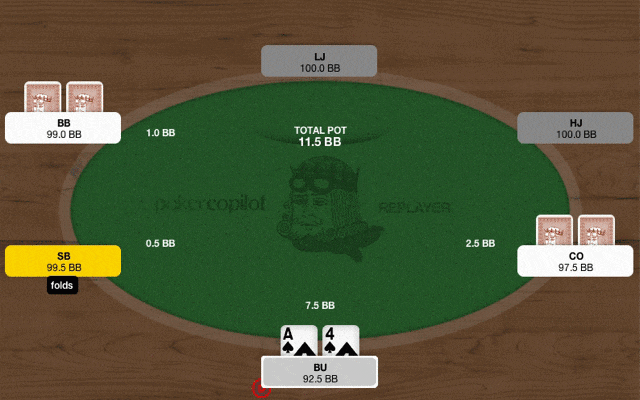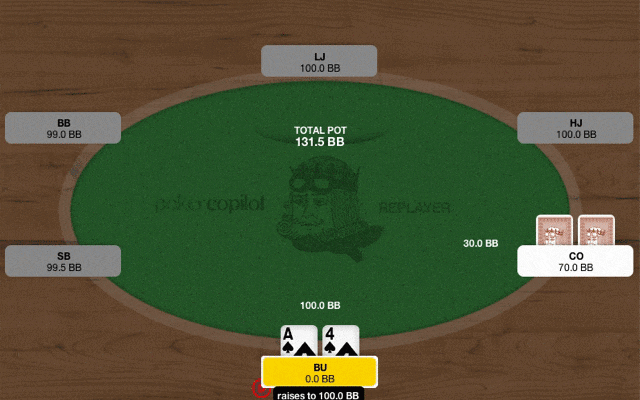
COが2.5bbにオープン、BUはA4sでブラフ3ベットを打ったところ、COから4倍のサイズの4ベットが返ってきました。
それに対してBUはブラフ5ベットオールインを選択しました。
COの4ベットに対してフォールドするとEV=0ですので、BUのブラフオールインのEVがもし少しでもプラスであれば、このオールインは正当化されます。
では、実際にこのブラフオールインのEVを計算してみましょう。
- EV(all-in)
=(COがフォールドする確率)*(BUの利益・損失)
+(COがコールする確率)*(COが勝利する確率)*(BUの利益・損失)
+(COがコールする確率)*(BUが勝利する確率)*(BUの利益・損失)
この式は前回説明したEVの計算式と同じで、まずは起こり得るすべてのシナリオを場合分けし、それぞれが起こる確率とその利益・損失を掛け算し、合計したものになっています。
まずはCOのハンドレンジを設定します。今回は{99+, AK, ATs, A3s, A2s, KQs}でCOは4ベットを打っているようです。AをBUが持っている(ブロックしている)ことを考慮して、このレンジのコンボ数は58です。
5ベットオールインに対してCOがコールするレンジは{AA, KK, QQ, AK}の27コンボとします。
フォールドするレンジは{JJ, TT, 99, ATs, A3s, A2s, KQs}、こちらは31コンボだとしましょう。
COがコールする確率は27/58*100=46.5%なので、フォールドする確率は100%−46.5%=53.5%となります。
また、COがコールした場合の勝率は、{AA, KK, QQ, AK}とA4sを比べればいいので、次のような勝率になります。

BUのA4sの勝率は約30%、COのレンジの勝率は約70%となり、大幅にCOが有利なようです。
次に、BUの利益・損失を明らかにしましょう。
COがフォールドした場合、BUはポットの131.5bbを利益として得ます。
また、オールインというアクションに必要な出費の92.5bbが損失として計上されますので、131.5bb−92.5bb=39bb、つまりオールインする前のポットサイズをBUは得ることになります。
COがコールし、なおかつCOが勝った場合、BUの利益は当然ゼロで、損失はオールインに使った92.5bbとなります。
COがコールし、なおかつBUが勝った場合、BUの利益はポットの201.5bbで、損失はオールインに使った出費の92.5bbですので、201.5bb−92.5bb=109bbを得ることになります。
これですべての数字がそろいましたので、EVの計算式に代入していきます。
- EV(all-in)
=(53.5%)*(39bb)
+(46.5%)*(70%)*(−92bb)
+(46.5%)*(30%)*(109bb)
=20.865bb−29.946bb+15.2055bb
=6.1245bb
となり、+EVであることがわかりました。
BUはフォールド(EV=0)よりもブラフオールインをしたほうが期待値が高いのです。
この結果からはいろいろなことが学べます。
まず、COはもっと広いレンジでBUのオールインにコールしなければならないかもしれませんし、あるいはブラフ4ベットを打つレンジ{99, ATs, A3s, A2s}を変えたり、4ベットのサイズを見直すべきかもしれません。
また、BUの視点から考えることもできます。
まず、この5ベットオールインのEVがここまで高いのは、A4sが相手のAをブロックしているためです。
Aが1枚既に見えているため、COがオールインにコールするAA、AKのコンボ数が7コンボも減っています。
もし、JTsや55のようなハンドで5ベットオールインをすると、COがコールするコンボ数はより多くなり、十分なフォールドエクイティが稼げない可能性が高いでしょう。
また、A4sはCOがコールするレンジのうち、AA以外のハンドに30%前後の勝率があります。この点も優秀です。
仮にCOがブラフ4ベットが少なく、{AA, KK, QQ, AKo}などの非常に狭いレンジでのみ4ベットを打っているとすると、十分なフォールドエクイティが得られないため、恐らくBUのブラフオールインは−EVになると予想できます。
そのようなnitなプレイヤーに対しては5ベットブラフは明らかにEV<0なので、COの4ベットには単にフォールドするか、あるいはそもそもA4sで3ベットを打たないのも手です。
このようにさまざまな状況を想定してオールインのEV計算をすることは、その計算結果から類推して考えたり、あるいはよりEVの高い戦略を構築するのに役立つでしょう。
コンティニュエーション・ベット(CB)の簡易的なEV計算
ポーカーではプリフロップでオールインするような状況よりも、ポストフロップで戦うことのほうが圧倒的に多いです。
ここでは特にフロップでCBのEVを簡易的に計算してみようと思います。
ここでも具体的な状況を考えてみましょう。
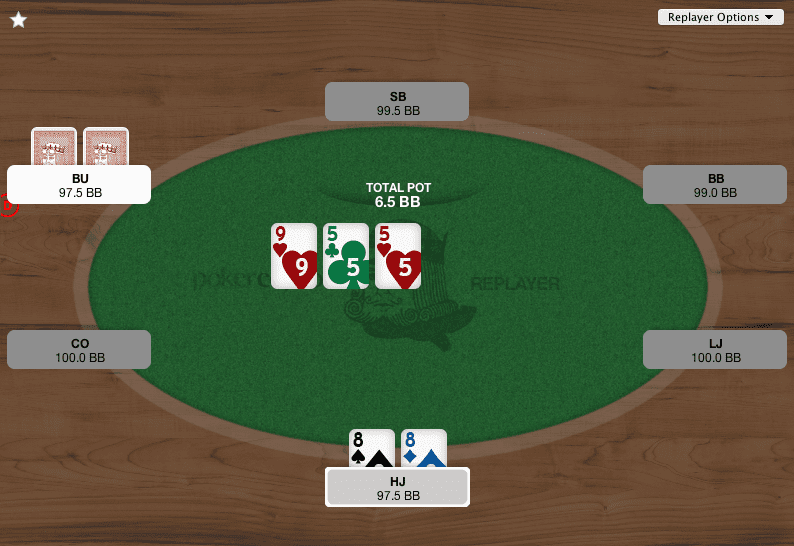
HJは88でオープン、BUのみがコールしてヘッズアップです。
上の画像のようなフロップが開き、HJはCBとチェックの選択ができます。
この場合のCBのEVを簡易的に計算してみたいと思います。(CBのベットサイズは3.5bbとします)
HJがCBを打った場合、以下の三つのシナリオが考えられます。
- BUはフォールドする
- BUはコールする
- BUはレイズする
ところで、2番と3番は本来さらに未来のシナリオがあるはずです。
つまり、BUがコールするとターンのカードが落ち、HJのアクションがあり、それに対するBUのアクションがあり・・・という具合です。
3番の場合も同様で、BUのレイズに対してHJのアクションがあり・・・となります。
シナリオの分岐はほとんど無限にあり、もちろんそのような複雑なEV計算は現実的ではありません。
そのため、ここでは「未来のシナリオにおいて、HJは必ずエクイティを最大限実現できるようなアクションを選ぶ」と仮定します。
未来のシナリオの中にはプレイが難しいものがあり、状況によってはどうしてもエクイティを捨てざるを得ないこともあるでしょう。
理想的にはそうした状況も含めてEV計算をしたいところですが、計算が複雑になりすぎるため、今回はそうした状況は無視し、それによってシナリオを三つのみ(BUはフォールド・コール・レイズ)に限定して簡易的なEV計算を行います。
簡易的なCBのEV計算式は以下のようになります。
- EV(CB)
=(BUがフォールドする確率)*(HJの利益・損失)
+(BUがコールする確率)*(HJの利益・損失)
+(BUがレイズする確率)*(HJの利益・損失)
まず、EVを計算するためにはHJの勝率(エクイティ)を知る必要があります。勝率はもちろんBUのレンジによって変化しますので、ここではBUのプリフロップのコールレンジを次のように設定します。
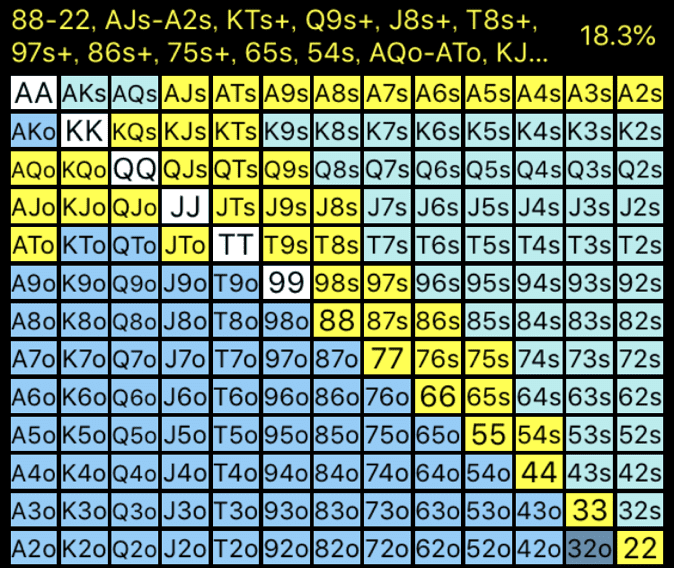
BUはAQs+や強いポケットペアを3ベットに回し、多くのスーテッドハンド、ミドル以下のポケットペア、AXでコールしています。
これは全ハンドの18.3%に相当し、かなり広いコールレンジです。
このコールレンジに対してHJの88はプロップで67%の勝率があります。非常に高い勝率です。

では次に、各シナリオを一つずつ見ていきます。
まずはHJのCBに対してBUがレイズしてきた場合を考えてみましょう。
BUは自分のレンジのうち、フラッシュドロー・5のトリップス・5のクワッズをレイズに回すと今回は考えます。
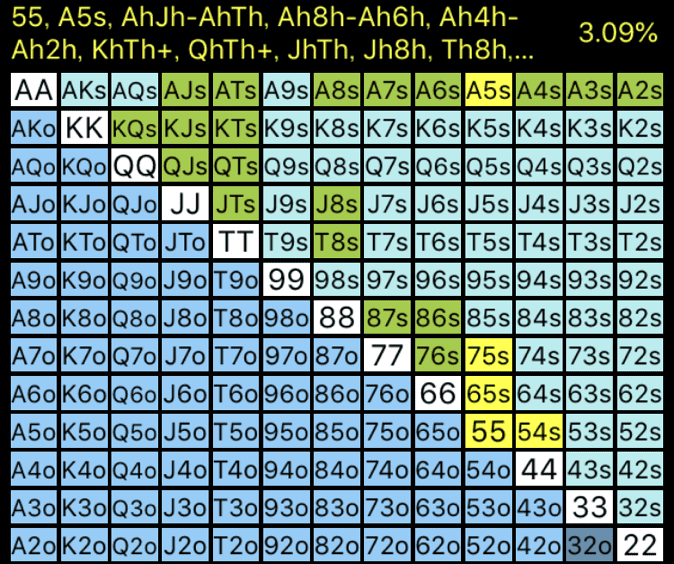
緑色はハートのスーテッド、黄色は可能なコンボ数すべてです。
コンボ数は全ハンドの3.09%ですので、BUがレイズするのは彼のレンジのうち16.8%であることがわかります。(3.09/18.3*100=約16.8%)
このようなレンジでレイズされた場合、HJはOOPであるため戦いにくく、またBUのコンボドローやオーバーカード+フラッシュドロー対してもあまりエクイティは高くなく、さらにBUが5を持っていた場合にはほとんどドローイングデッド(勝率がゼロ)です。
そのため、CBに対してBUがレイズしてきた場合には、HJは素直にフォールドすることにします。
ですので、この場合のHJの利益・損失はCBに使った出費の3.5bbとなります。
次に、CBに対してBUがコールした場合を考えてみましょう。
BUは自分のレンジのうち、9のペア、55以外のすべてのポケットペアをコールに回すと今回は考えます。
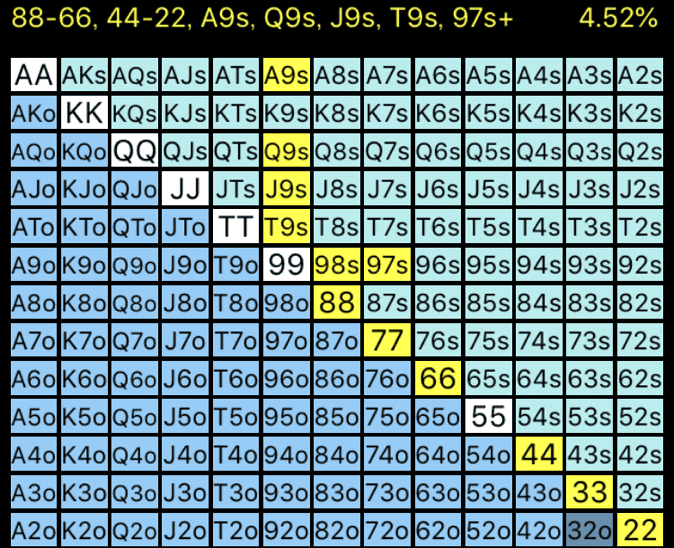
コンボ数は全ハンドの4.52%ですので、BUがコールするのは彼のレンジのうち24.7%であることがわかります。(4.52/18.3*100=約24.7%)
CBをBUにコールされた場合、BUとHJ(88)の勝率は次のようになります。
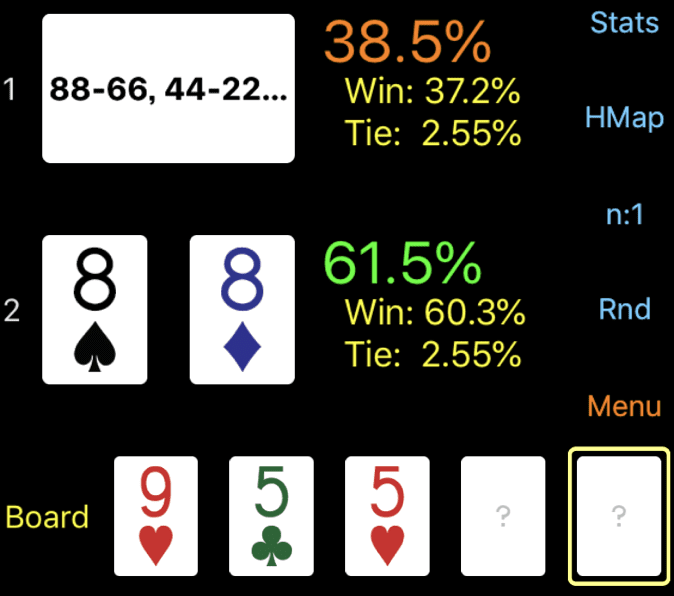
フロップが開いた時点の勝率67.3%から少し下がったとはいえ、61.5%とまだかなり高い勝率があるようです。
この場合のHJの利益・損失を計算します。
CBをコールされたことによりポットが(6.5bb+3.5bb+3.5bb)=13.5bbとなり、エクイティが61.5%ですので、13.5bb*61.5%=約8.3bb:これがHJの利益です。
そこから出費(損失)の3.5bbを引いて8.3bb−3.5bb=4.8bbとなり、これがCBにコールされたときのHJの利益・損失となります。
最後に、BUがCBに対してフォールドした場合を考えてみましょう。
先ほどのBUがレイズorコールするレンジの割合から考えて、BUがCBに対してフォールドするのは彼のレンジのうち58.5%であることがわかります。(100%−16.8%−24.7%=58.5%)
この場合のHJの利益・損失を計算します。
獲得するポットは6.5bb+3.5bb=10bb(利益)で、そこから出費の3.5bb(損失)を引くので、結局フロップが開いた時点のポットである6.5bb、これがCBに対してBUがフォールドしたときのHJの利益・損失となります。
さて、ようやく必要な数字がすべてそろいましたので、EV計算式に代入していきます。
- EV(CB)
=(58.5%)*(6.5bb)
+(24.7%)*(4.8bb)
+(16.8%)*(−3.5bb)
=4.4bb
これがHJのCBのEVです。3.5bbのCBのEVが4.4bbというのは極めて高い数字です。
EVが高くなっている理由はいくつかありますが、そもそもBUのプリフロップのコールレンジが極めて広く、そのレンジのほとんどが88に負けていることが最大の理由です。
この結果からわかるように、BUはプリフロップのコールレンジを狭くしたり、ブラフ3ベットをするレンジを作る必要があるかもしれません。
前者の場合、特にAToやJToのような投機性のないハンドや、22や33などの弱いポケットペアはプリフロップのコールレンジから消えることになるでしょう。
また、AAやKKのようなバリューの3ベットとバランスを取るかたちで、KQsやA4sなどのブラフに適しているハンドをブラフ3ベットに回すべきかもしれません。
実際、バランスの取れた以下のようなコールレンジの場合、同じフロップでもHJの88はCBを打つことができません。CBのEVが非常に低く、チェックのEVのほうが高くなるからです。
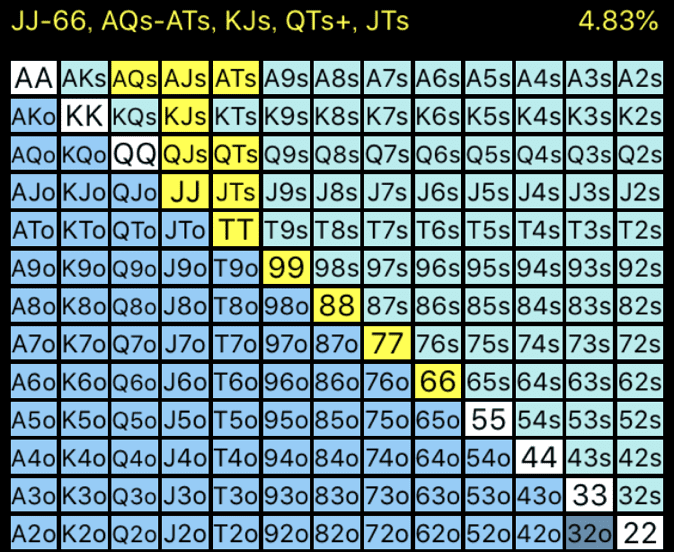
今回と同じようにEV計算をするとわかりますが、プリフロップでこのようなコールレンジでIPからコールされた場合、HJのアクションで最もEVが高いのはチェックです。
このように簡易的ではありますが、いろいろな状況のCBのEVを計算しておくことは、ポストフロップ戦略だけでなくプリフロップのコールレンジやブラフ3ベットレンジを構築する際にも役立ちます。

コメント
コメント一覧 (3件)
諸々の計算やレンジ表に使っているアプリの名前は何ですか?
>>あさん
PokerCruncherのMac Expert VersionをiPhoneとmac bookで使っています。
ありがとうございます!