【資料集】ポーカーのいろいろな確率

勝率・オッズとは？

ポーカー用語の「勝率」とは文字通り「あるハンドがショーダウンで勝つ確率」のことです。例えばAAとKKがプリフロップでオールインになったとき、AAの勝率は約81％です。

一方で「オッズ」とは、「ポットに参加するために必要なチップと、勝ったときに得られるポット比率」のことです。投資と見返り、リスク・リターンとも言えます。オッズに見合った額のチップを賭けると、リスク・リターンのバランスを取ることができ、長期的に見て少しずつ得をしていくか、少なくともプラスマイナスゼロの状態になります。

もう少し詳しくオッズについて見てみましょう。
例えば、相手がリバーでポットサイズのベット（1ポットのベット）をしてきて、それに自分がコールする場合を考えましょう。この場合のオッズは次のようになります。

• 「ポットに参加するために必要なチップ」は1ポット
• 「勝ったときに得られるポット」は場に出てるチップすべてなので、
  （相手がベットした1ポット＋もともとあった1ポット＋自分がコールした1ポット）＝計3ポット

ですので、この場合のオッズは1/3、つまり約33.3％ということになります。別の言い方をすれば、「3回に1回勝てば元が取れる」ということになります。
自分のハンドとボードを見比べて、自分に33.3％以上の勝率がありそうだと思えば、相手の1ポットのベットにコールすることができます。もちろん、実際は相手のハンドのほうが強く、ショーダウンで負けてしまうこともあります。しかし、同じようにオッズが33.3％の状況で、33.3％以上の勝率でショーダウンすることは今後もあるでしょう。そうすると、短期的な勝ち負けはあるものの、十分長い目で見れば徐々に利益が増えていくか、少なくともプラスマイナスゼロに落ち着くはずです。

• 1ポットを投資して3ポットが返ってくる＝3回に1回勝てば元が取れる
• 自分の勝率は約33.3％＝3回に1回は勝てる

前のストリートで賭けたチップは考える必要はありません。あくまでも「今、いくら投資すればいくら見返りがあるのか」に注目すべきです。
例えば、プリフロップではなく、リバーからいきなり始まるポーカーを考えてみてください。そのポーカーの1回の参加費は高く、さっきの単位で言うと0.5ポットです。ヘッズアップで相手も0.5ポットを払っているので、テーブルには合計1ポットがあります。そこに相手が1ポットのベットをしてきました。自分のハンドとボードを見比べると、勝率は3回に1回勝てるぐらいだとします。ここだけを見れば、さっきの例と全く同じ状況です。ということは、このリバーから始まるポーカーでコールをするのが正しいなら、さっきの例でも同じようにコールをすべきでしょう。

そうです。未来の損得を決めるのは、あくまでも現在の状況判断です。過去に自分がどんなアクションをしたか、どれだけのチップを賭けたのかは関係ありません。これはポーカー用語ではありませんが、すでに支出してしまって回収できない費用のことを「サンクコスト（sunk cost）」といいます。「埋没した費用」という意味です。
例えば、休日に映画館に行くというケースを考えてみます。チケットを買っていざ映画が始まると、なんだか期待していたほど面白くありません。座っているのがだんだん苦痛になってきました。でも、ここで映画を見るのをやめてしまうとチケット代と貴重な休日が無駄になってしまうと思い、エンドロールまで見続けました。しかしやはり最後まで駄作で、こんなことなら別の映画にすればよかった、いや久しぶりの休日だったからもっと有意義なことをすればよかったと後悔するわけです。この場合、チケット代と映画が面白くないと気づくまでに費やした時間がサンクコストです。チケット代と時間は絶対に戻ってくることはないにもかかわらず元を取ろうとして映画を見続け、その結果、時間的・精神的損失が大きくなってしまったというわけです。チケット代と時間はスッパリ忘れてしまって、映画の途中で映画館を出て買い物をするなり、自宅に戻って掃除をするなりしたほうがいい休日になったかもしれません。
このように、サンクコストを惜しむのは人間の先入観によるもので、未来の損得を合理的に判断するためにはサンクコストを無視しなければなりません。「やっちまったもんはしょうがない」の精神で、それから先の利益を考えることが大事なのです。サンクコストは時間、金銭、労力など、さまざまな形で日常に現れます。高額だったけど効かないダイエット食品、ソーシャルゲームの課金、そしてポーカーにおいては前のストリートで賭けたチップがサンクコストです。

「オッズに合う」とは、「自分のハンドの勝率がオッズよりも高いこと」を指します。さっきの例で言えば1/3＝33.3%がオッズで、自分のハンドの勝率が33.3%あったので、ぎりぎりオッズに合うということになります。オッズとは投資するチップと見返りの比率ですから、その比率と同じ勝率があれば、長い目で見て損はしないということです。もちろん、オッズよりも高い勝率があれば、繰り返しプレイすればするほど利益が大きくなっていきます。

アウツとは？

「アウツ」とは、「自分のハンドをより強い役にするようなカード」のことです。
例えば、KQを持っていて、ボードがA83なら、ターンかリバーでハートが落ちればナッツフラッシュが完成します。この場合、Jから2までの残り9枚のハートのカードがフラッシュのアウツです。
アウツという言葉はフラッシュやストレートのドローを持っているときに特によく使われますが、ペアやハイカードの場合でももちろんアウツはあります。
例えば、AJを持っていて、ボードがJT5なら、残り3枚のAと2枚のJが自分のアウツとなり、現状のJペアAキッカーをツーペアやトリップスに進展させます。

アウツを引く確率

アウツの枚数とアウツを引く確率の対応表です。「ターンだけ」はフロップの段階でターンの1枚でアウツを引く確率、「ターンとリバー」はターン、リバーの2枚でアウツを少なくとも1回引く確率です。

アウツの枚数	ターンだけ	ターンとリバー
20	42.6%	67.5％
19	40.4%	65%
18	38.3%	62.4%
17	36.2%	59.8%
16	34.0%	57%
15	31.9%	54.1%
14	29.8%	51.2%
13	27.7%	48.1%
12	25.5%	45%
11	23.4%	41.7%
10	21.3%	38.4%
9	19.1%	35%
8	17.0%	31.5%
7	14.9%	27.8%
6	12.8%	24.1%
5	10.6%	20.4%
4	8.5%	16.5%
3	6.4%	12.5%
2	4.3%	8.4%
1	2.1%	4.3%

例えばフラッシュドローですとアウツが9枚ありますので、ターンで引くならば19.1%の確率です。

簡単な計算方法があります。アウツの枚数に2をかければターンだけで引く確率、4をかければターンとリバーで少なくとも1回引く確率とほぼ同じ値になります。 例えばフラッシュですと、アウツが9枚なので9枚かける2＝18で、19.1%に割と近い値が出ます。
表のアウツの枚数に2、4をかけてみてください。右側の確率と近い値になります。

アウツの枚数が多いほど、この簡易計算の確率と実際の確率にズレが生じます。しかし、16枚以上のアウツを考えることは実戦の中ではほとんどありませんので、大きな問題はないでしょう。

実際にオッズとアウツを計算してみる

それでは、実戦でオッズ、アウツ、勝率を計算するにはどうすればいいのでしょうか。よくあるシチュエーションを一緒に考えてみましょう。

• あなた（BU）：AJ
• 相手（SB）：？？
• ボード：Q75
• ポット：7bb

プリフロップであなたはBUからAJで3bbをオープン、SBがコールし、BBがフォールドしました。ヘッズアップで、ポットは7bbです。
フロップではペアこそできませんでしたが、ナッツフラッシュのドローがあります。
SBがチェックしたので、自分は4bbをベットしたところ、相手は8bbにレイズしてきました。さて、このレイズにコールすべきでしょうか、フォールドすべきでしょうか。

相手のレイズに対して3ベットすると、自分のハンド（Aハイフラッシュドロー）よりも弱いハンドはフォールドし、逆に強いハンドはコールかさらにレイズをしますから、結局損してしまう可能性が高いと思います。

相手にもよりますが、基本的にはそうです。
さて、コールかフォールドかを判断するために、まずは自分がターンを見るのに必要な勝率、オッズを計算しましょう。
自分が相手のレイズにコールしたとき、場にあるすべてのチップ（ポット）は、
（もともとあった7bb＋相手のレイズした8bb＋自分がコールした8bb）＝23bb
となります。その23bbのポットに参加するためには追加で4bbをコールする必要があります。ということはオッズは4/23、23回に4回勝てばいい計算で、パーセントに直すと約17.3%です。
一方、ターンでフラッシュのアウツを引く確率は、ダイヤの残り9枚に2をかけて約18%です。これはオッズ（必要な勝率）の17.3%よりも高いので、オッズに合います。つまり、コールして問題なさそうです。また、仮に相手がQJのようなハンドでレイズしてきているなら、ターンでAを引いても勝てますから、Aのアウツ3枚をフラッシュのアウツ9枚に加えて、合計12枚のアウツがあると考えられます。その場合、ターンで自分が勝つ確率は24%となります。

もちろんあります。さっきの問題で、手持ちのチップが少ないSBがリレイズオールインしてきた場合を考えてみましょう。

そのとおりです。オールインのサイズは15bbとしましょう。この場合、オールインにコールすればリバーまで必ず見ることになりますから、ターン、リバーの両方でアウツを引く確率の計算をします。
自分が相手のオールインにコールしたとき、場にあるすべてのチップ（ポット）は、
（もともとあった7bb＋相手のオールインの15bb＋自分のコールした15bb）＝37bb
となります。そのポットに参加するために自分はあと11bb出す必要があります。つまり、11を出して37返ってくるオッズとなっており、必要な勝率は11/37＝約29%です。
ターンまたはリバーでフラッシュを引く確率は9枚かける4で約36％となり、これは必要な勝率の29%よりも高いので、やはりオッズに合います。これもコールして問題なさそうです。

そういうことです。基本的には、必要な勝率を満たさないハンドでコールすることは、長期的に見て損です。*1

覚えておくと便利な確率

フロップで役やドローができる確率やハンド同士の勝率は覚えておくと何かと便利です。いくつか代表的なものを挙げていきます。

※ポケットペアでないハンドを「XY」と表記します。確率の小数点以下は四捨五入しています。

フロップで役やドローができる確率

	確率	ハンドの例	ボードの例
XYのうち少なくとも1枚がフロップでペアになる確率	32%	AK	A82
XYの両方がフロップでペアになる確率	2%	AK	AK7
コネクタがフロップでストレートドロー（ガット、オープンエンド）になる確率	26%	QJ	T95
コネクタがフロップでストレートになる確率	1%	QJ	T98
スーテッドがフロップでフラッシュドローになる確率	11%	87	AJ3
スーテッドがフロップでフラッシュになる確率	1%	87	AJ5
ポケットペアがフロップでセットになる確率	11%	66	Q62

そのとおりです。それはとても大事なポイントで、コンティニュエーション・ベット（CB）が利益を生む最大の理由です。つまり、相手はフロップで3回に2回はペアを持っていないはずなので、ベットすれば相手はフォールドする可能性が高いということですね。コンティニュエーション・ベットはとても大事なトピックですので、別の回で詳しく説明します。

ポケットペア同士の勝率

およそ80%vs20%です。

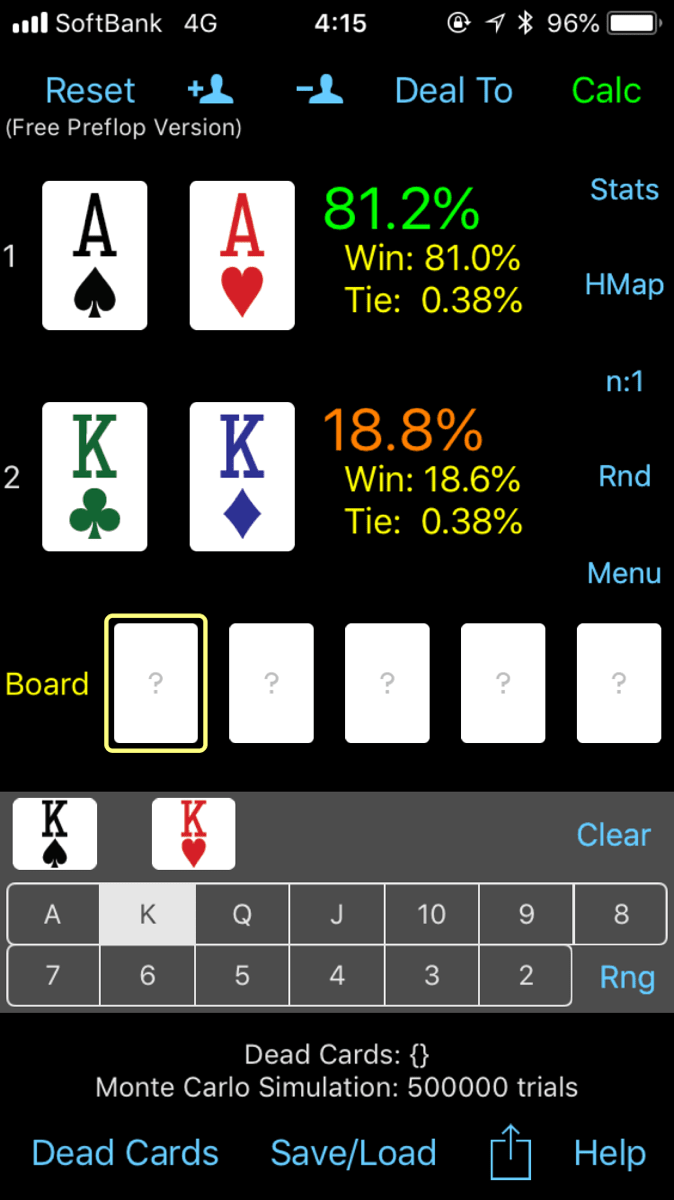
XY同士の勝率

オーバーカードが2枚あるならおよそ66%vs33%です。
コネクタ、スーテッドがつくとそれぞれ約4％ずつ勝率が上がります。
オーバーカードが1枚の場合はハンドによって確率が変動しますが、およそ60%vs40%が目安です。

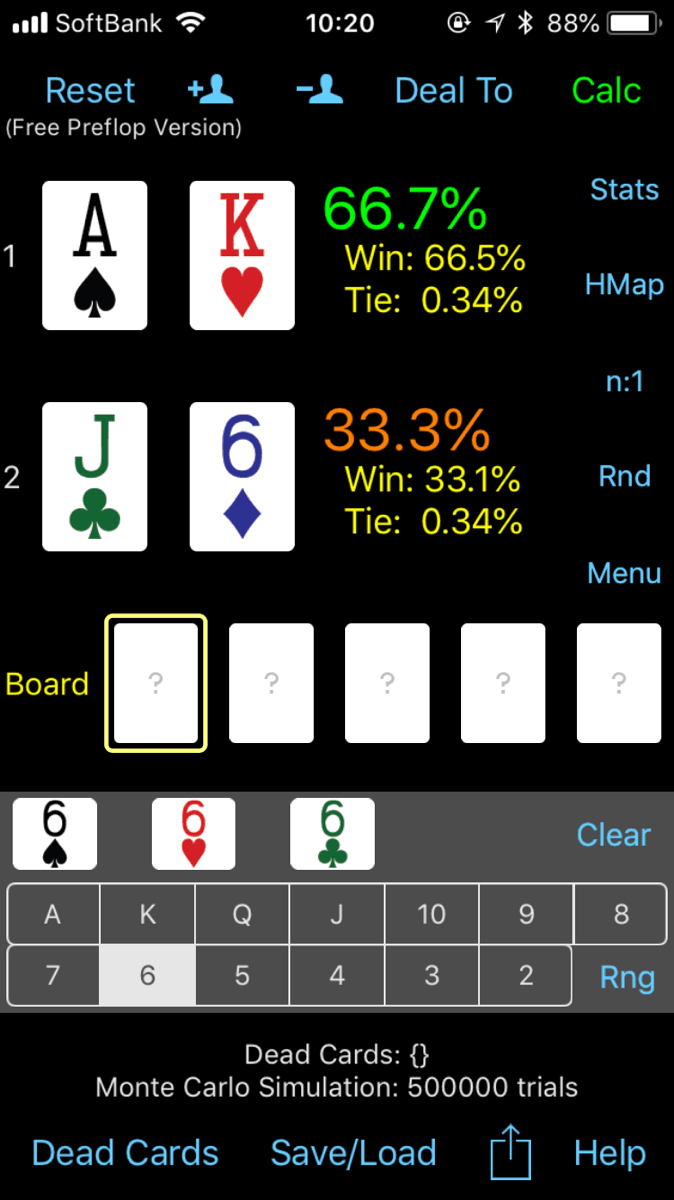
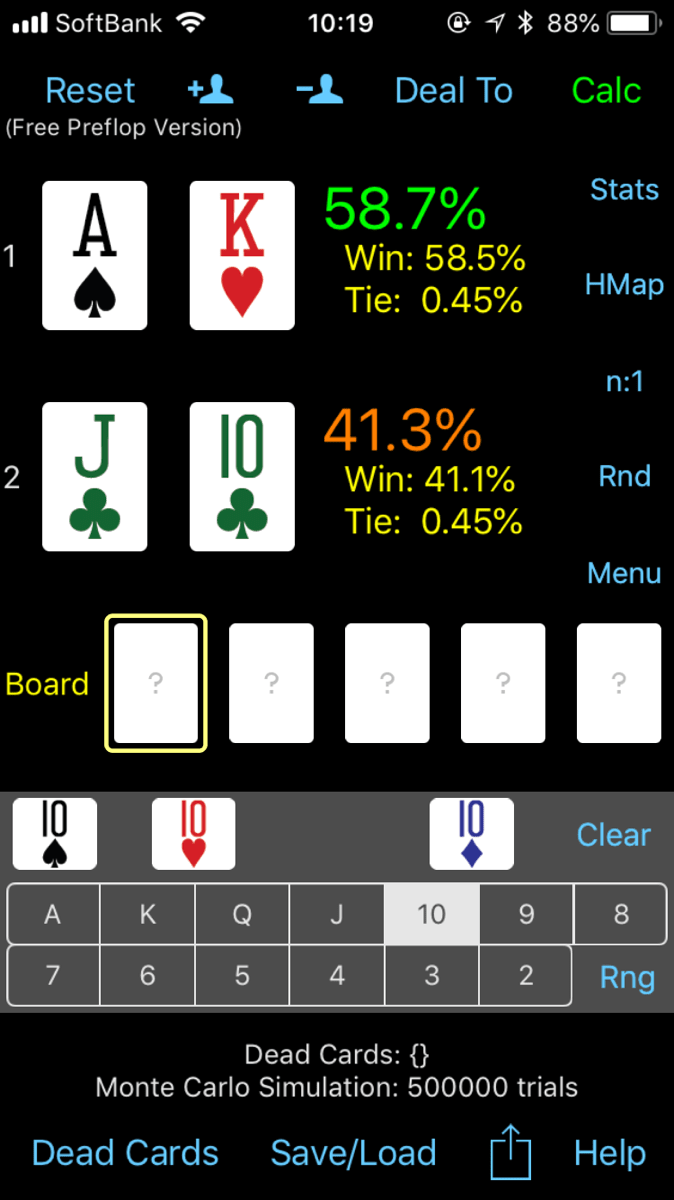
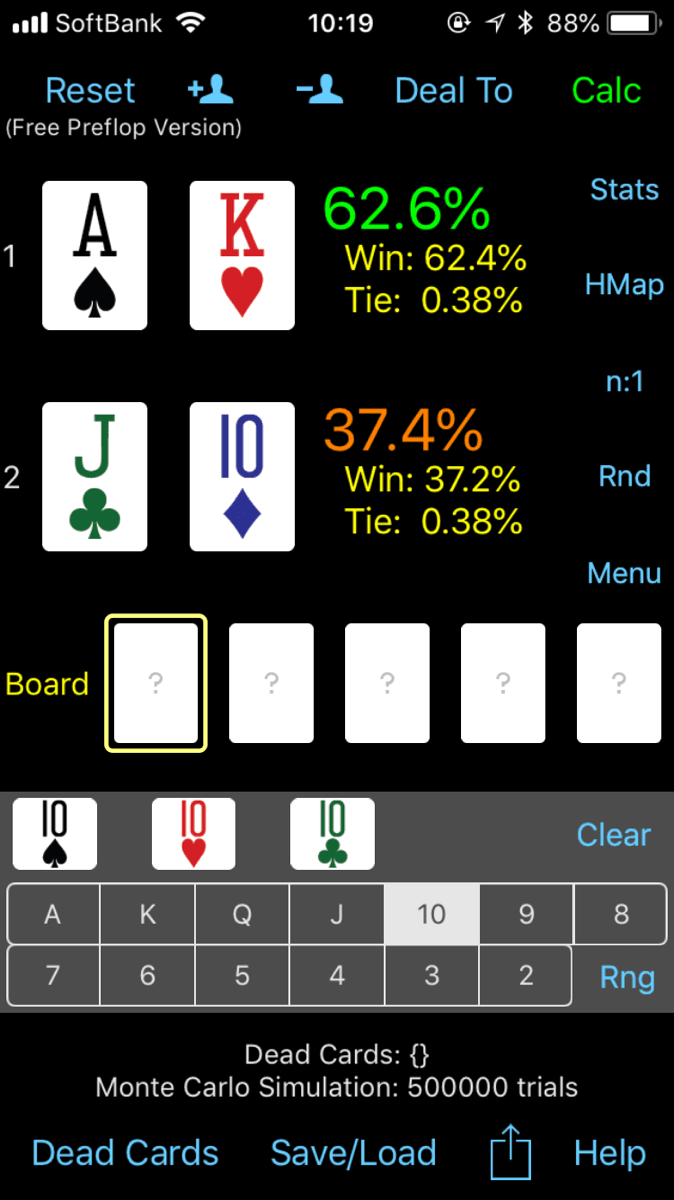
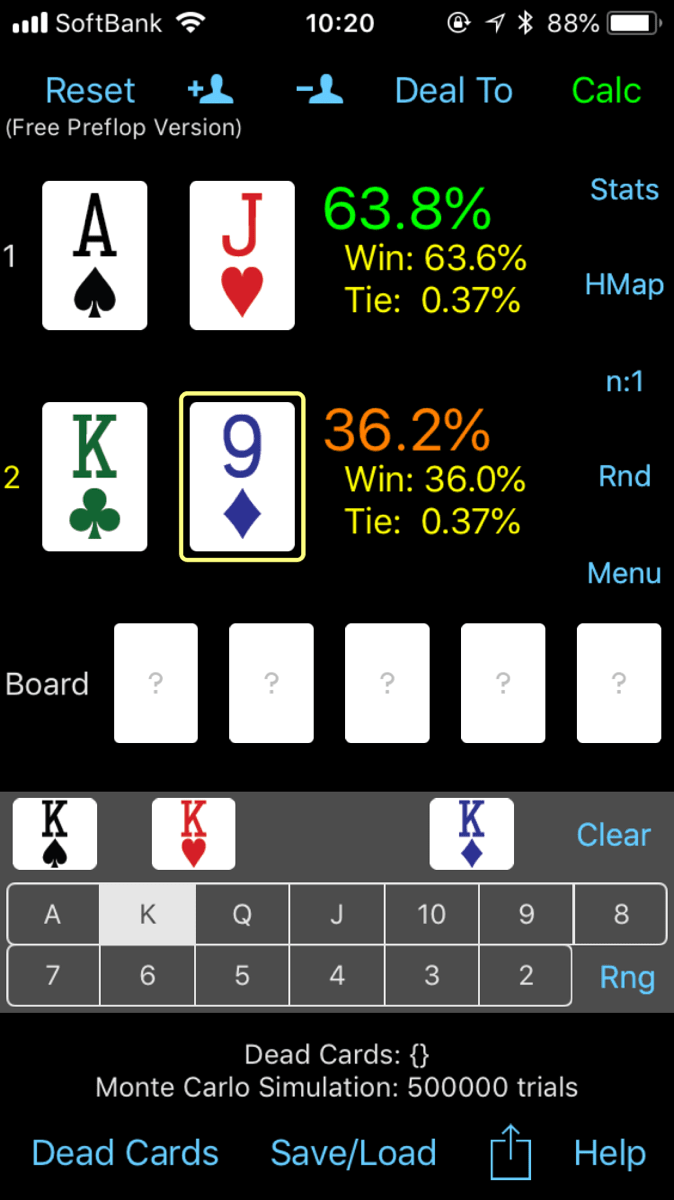
XYとポケットペアの勝率

XYとそれよりも低いカードのポケットペアの勝率です。
およそ45%vs55%でポケットペアに分があります。

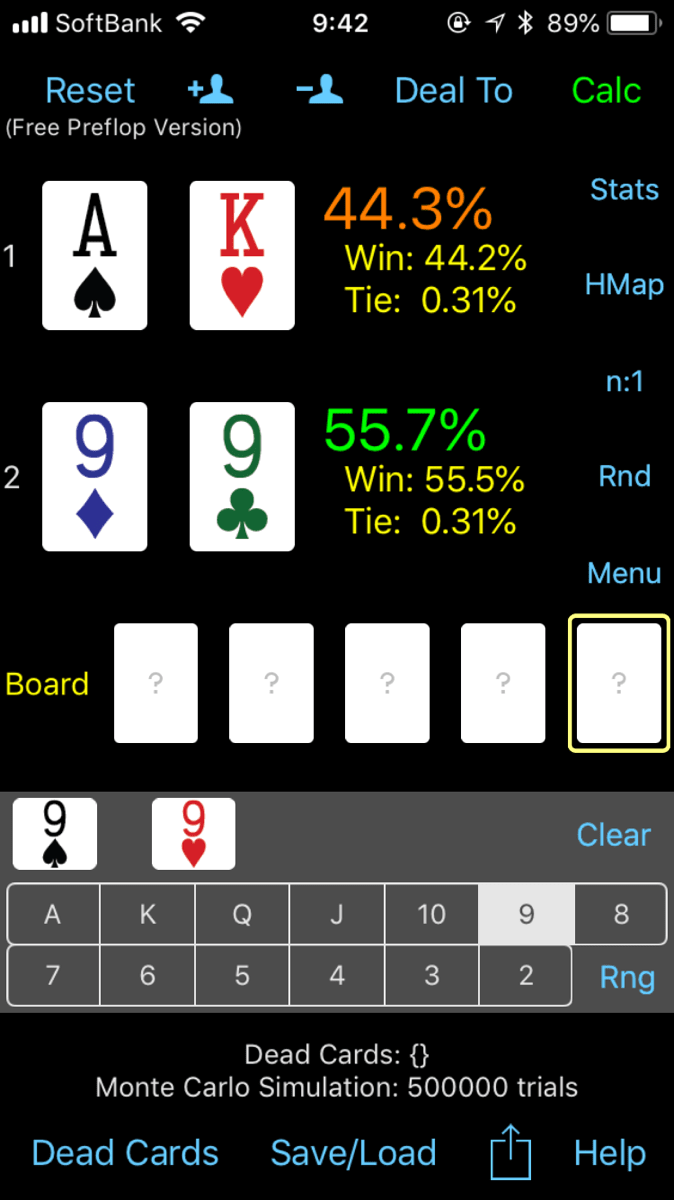
XY同士でキッカーをドミネイトしているときの勝率

XY同士でキッカーをドミネイトしている場合の勝率です。
およそ74%vs26%となり、ドミネイトしているハンドにかなり分があります。

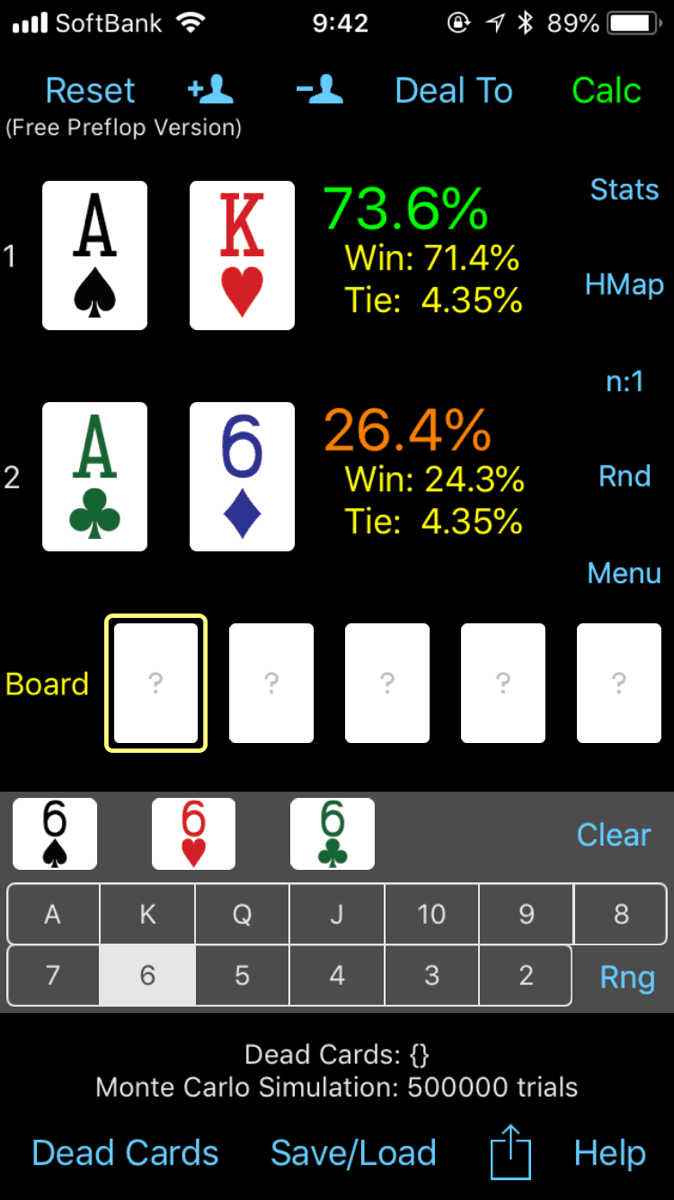
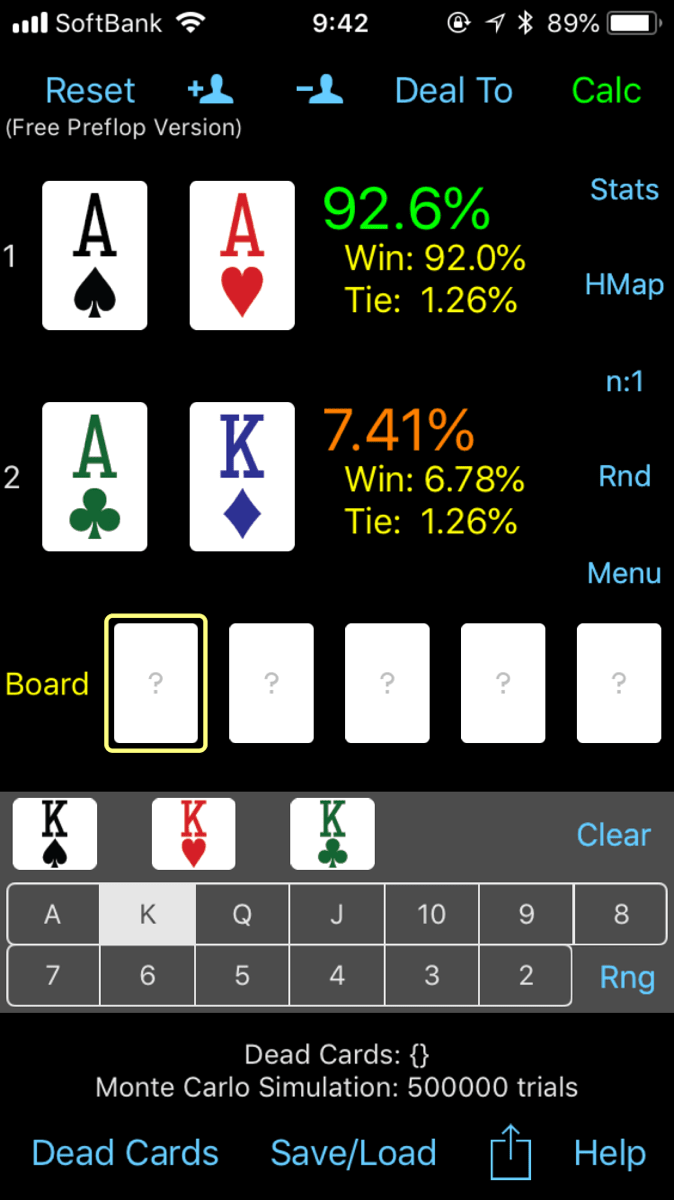
XXvsXY（AAvsAKなど）

ポケットペアとXYで、同じカードを持っている場合の勝率です。
およそ92%vs8%となり、ポケットペアが圧倒的に有利です。この場合だと、AKはKを2枚引くか、ストレートを作るか、AかKで4枚フラッシュを引くしか勝ち目がありません。